@philip asks a good question here because… before you can test your code, you need to know how to tell if it worked—they call this Test-driven development (TDD) in computer science.
So, for example, if you were writing a formula (perhaps in a Subroutine!) to calculate the circumference of a circle based on its radius (e.g. 2 x PI x radius), you’d want to sanity-check a few answers.
Zero’s always a good/easy one to check first. If you plug in 0 for your radius and get something non-zero for the answer, try again.
Also, 1 is often a good test case, you’d better get something around 6.28 for this circumference example.
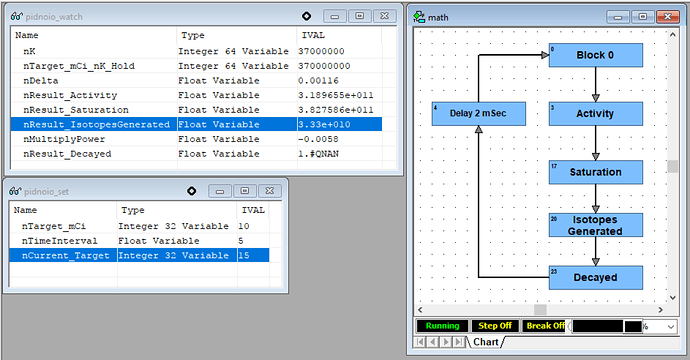
For the picture above, looks like for this formula circled in red, you’re trying to get a value for “d” (does this mean “population”)? Nice to use variables that are descriptive, and easier to search for, when you start coding. Also remember you get 50 characters so throwing in the units of measure (“iso” here for isotopes?) is sometimes a good idea, too. Ditto using lots of comments saying what the code is supposed to be doing.
Anyway, to calculate what I’ll call f_d_population, you apparently need values for what I’ll call: f_N_o , f_little_g, f_little_lamba, f_delta_t (what are all those?).
Note: I’m using naming convention here of a leading f_ because we’re going to use floats on the data types for all these (“why” on both of those I’ll leave for another thread).
Sometimes it helps to have other intermediate steps to see where something went wrong… I rarely get my complicated formals right on the first try!
This is true both when you’re checking your math by hand, and when you’re stepping through your code, with some known values (like we did with radius = 0 and radius = 1 on that circumference calc).
In this case, the value you’re raising e to would be one I’d create an extra variable for, perhaps called: f_e_exponent.
Perhaps also the coefficient there, (No + g) which I’ll call: f_e_coefficient
Looks like you have the one sample case (assuming the answers are correct), of:
Given: f_N_o = 319000000000.0, f_little_g = 33300000000.0, f_little_lamba = 0.00116, f_delta_t = 5
We expect: 2040000000.0 for our calculated d, based on what I’m seeing in the picture.
When I check this by hand, I get, starting with that exponent and coefficient:
f_e_exponent = -1 * f_little_lamba * f_delta_t
f_e_exponent = -1 x 0.00116 x 5 = -0.0058
f_e_coefficient = 319000000000.0 + 33300000000.0 = 352300000000.0
So e raised to that exponent = 0.9942, and when we multiply that by 352300000000.0, I get: 350256660000.0
Which is NOT the 2040000000.0 we expected, so I’m guessing that’s why @philip asked, wondering what he got….
I hesitate to hand you the proverbial fish here (the OptoScript I came up with) since that gave me roughly the same answer, but here it is anyway:
// initialize the example values
f_N_o = 3.19e11;
f_little_g = 3.33e10;
f_little_lamba = 0.00116;
f_delta_t = 5.0;
// do the calculations
f_e_exponent = -1 * f_little_lamba * f_delta_t;
f_e_coefficient = f_N_o + f_little_g;
f_d_pop = f_e_coefficient * RaiseEToPower(f_e_exponent);
Perhaps the person that wrote all this up can help clarify what’s off in what I have above?
Also, because I can’t resist a corny joke, did anyone notice how, in her OptoScript formula, OptoMary had an f_little_lamba (whose fleece was white as snow?) Har har, so sorry, couldn’t resist there…